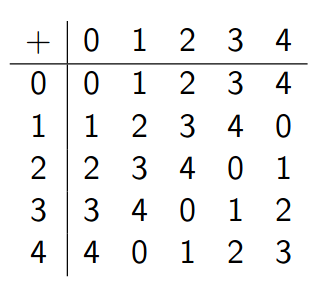Wiki/fhtw-bif04-ss2018/matu/20180228.md

Zahlentheorie

Kongruenz

Bei kongruenten Zahlen ist die Differez durch den Rest teilbar.

Restklasse

Alle Zahlen einer Restklasse sind kongruent.

Rechnen im Z_m

Gruppe

Menge + eine Verknuepfunge.

sodass:

• assoziativ
• neutrales Element
• zu jedem Element gibt es inverses Element

Bei Abelscher Gruppe:

• kommunitativ Gesetz

	Z+	Z*
assoziativ	✓	✓
neutrales Element	✓	✓
zu jedem Element gibt es ein inverses	✓	zu 0 kein mult, Inverses
kommutativ	✓	✓

Z_10 ist keine Gruppe.

Z_10\{0,2,4,6,8,5} ist eine kommunitative Gruppe.

Koeper

Menge mit 2 Verknuepfungen.

• Menge M
• Verknuepfungen +, *
• (M, +) ... kommutative Gruppe
• (M\0 *) .. kommutative Gruppe
• distributiv Gesetz: a * (b + c) = (a * b) + (a * c)

Beispiele:

• (Z_5, +, *) Koerper

• (Z_10, +, *) kein Koerper weil K_10, * keine Gruppe

• allgemein (Z_p, + *) ist ein Koerper

negatives / additives Inverses in Z_m

26 - 3 = 23

-3 = 23

Kehrwert / multiplikatives Inverses in Z_m

Kehrwert von a in Z_m existiert <=> a und m teilerfremd

ggT(a, m) = 1

Berechnet mit erweitertem Euklidischen Algorithmus.

Eulersche phi-Funktion

kleiner Satz von Fermat